Nedir Bu Vites Oranları Dedikleri?

Yazar:

Bir okurumuz, mektubunda, vites oranlarının neyi ifade ettiğini sormuş. Hazır vites konusu açılmışken biraz daha geriye gidip dişlilerden anlatmaya başlayalım istedim. Belki biraz ortaokul konuları olacak ama sabır göstereceğinizden eminim. Buyurun, buyurun… biz de daha yeni başladık konuya; tam zamanında geldiniz. Önde boş koltuklar var, bu tarafa da oturabilirsiniz.

Yetkisiz Servis

Motoron Dergisi Yazarı

önce dilbilgisi:

Türk Dil Kurumu, “dişli” sözcüğü için “Dişleri olan” ve “Dişleri olan çark” tanımlamasını kullanmış Pekiyi çark nedir diye merak ettiğimde verilen tanım ise aynen şöyle: “Bir eksenin döndürdüğü tekerlek biçimindeki makine parçası. Dişli, dişleri olan çark.”

Dolayısıyla çark veya dişli olarak kullanacağım ifadeyi, bir eksen etrafında dönen ve genellikle çevresinde dişler olan makine parçası olarak algılamakta fayda var. Kafanız karışırsa her zaman, tekrar bu tanımlara bakabilirsiniz.

nerede bu dişli?

Bir eksen etrafında dönen parçaların çoğunda dişliler vardır. Otomobil ve motosikletlerimizin motorlarında ve vites kutularında bir çok dişli çalışır. Dişliler, hareket enerjisi üretilen hemen her yerde bulunurlar. Bulunurlar bulunmalarına da ne işe yaralar pekiyi?

Dişliler, genel olarak 4 değişik amaçla kullanılır:

Dönüş yönünü aksi istikamete çevirmek için

Dönüş hızını arttırmak veya yavaşlatmak için

Hareket enerjisini, bir başka eksene taşımak için

İki ayrı eksenin hareketlerini eşgüdümlemek (senkronize etmek) için.

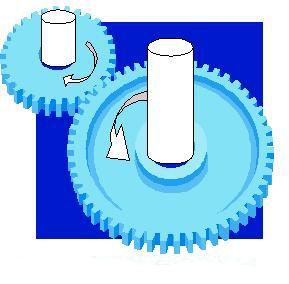
1 numaralı resimde, saydığımız 4 amaçtan ilk 3 tanesini gözlemleyebilirsiniz:

1) Her iki dişli farklı yönlerde dönmekte,

2) küçük dişli, büyük dişliden daha çok tur atarak daha hızlı dönüyor,

3) Bir dişilinin eksenindeki hareket enerjisi, diğer dişlinin eksenine yönleniyor. Yani küçük dişlinin eksenini siz çevirirseniz, eksene bağlı olan küçük dişliyi çevirmiş olursunuz. Küçük dişli, büyük dişliyi ve ona bağlı ekseni çevirmiş olacak. Yani, hareket enerjisini bir eksenden (bir akstan, bir kaynaktan) diğer eksene (aksa, hedefe) aktarmış olduk.

Bu resimdeki küçük dişli, büyük dişliye göre daha hızlı dönmektedir. Böyle bir hız değişikliğinin sebebi, her iki dişlinin çevrelerinin birbirinden farklı olmasıdır. Eğer dişlilerin çevreleri aynı olsaydı, her birisi farklı yönlerde ama aynı hızda döneceklerdi.

Dişli oranlarını çözmenin yolu, çemberin çevresini ölçmekten geçer. Okul bilgilerinizi tazeleyin bakalım. Dairenin çevresi, daire çapının Pi sayısı (3.14159…) ile çarpımıyla bulunur. Dolayısıyla, çapı 1 santimetre olan bir dairenin çevresi, 3.14159 santimetre olacaktır. Şimdi bir başka örnek verelim: Çapı 1.27 metre olan bir çemberimiz var. Bu çemberi yerde yuvarlarsanız, çember yerde bir tam tur attığında kaç santimetre yol almış olur? (Hımmmm…. 1.27 çarpı 3.14… eşittir 4 kere 7 eşitti 28, elde var 2… Üffff… Hesap makinesini nerede ya?) Tamam söylüyorum, 4 metre yol alır. Çemberin çapını iki misline çıkartalım ve yerde yuvarlayalım. Tam bir tur attığında, daha küçük çembere göre iki misli fazla yol alacaktır. Birbirinden farklı büyüklükteki dişliler de aynı prensiple çalışır ve dişli oranı diye bahsettiğimiz farklılıkları meydana getirirler. Çapları ve/veya çevreleri ölçüldüğünde biri diğerinin tam olarak iki misli olan iki dişlinin birlikte hareket ettiğini düşünün. (Hayal gücünüzü canlandırmak için 1 numaralı resme bakabilirsiniz.) Küçük dişlinin çevresi 1, büyük olanınki 2 metre olsun. Her ikisi de aynı miktarda yol alsınlar; aynen çember örneğindeki gibi. Küçük olan iki tur atar ve 2 metre giderken büyük dişli 1 tur atarak 2 metre gidecektir. İşte böyle bir durumda küçük olan dişlinin büyük olana oranı 2’ye 1 olarak adlandırılır. Bu söyleyiş şekli, 2:1 olarak gösterilir. Büyük dişlinin küçük dişliye olan oranını ifade edersek de tersten söyleriz; yani 1’e 2 veya 1:2.

çarklar kimin için çalıyor?

Hareket eden çarkların çoğunda “diş”ler bulunur. Dişlerin üç temel avantajı vardır:

• Her bir çarkın, diğer çarktan kaymasını önlerler. Dolayısıyla, çarklar vasıtasıyla birbirlerine bağlanan eksenler, birbirleriyle tam bir eşgüdüm (senkron) içerisinde dönerler.

• Dişli oranlarının tam olarak belirlenmesine olanak sağlarlar. Yani, her iki çark üzerindeki diş sayılarını hesaplayıp diğerine bölerek dişli oranlarını bulabiliriz. Bir çark üzerinde 60 adet diş, diğer çarkta ise 20 adet diş varsa, birbirine bağlanmış iki çarkın dişli oranı 3:1 ‘dir.

• Dişliler sayesinde, çarklar üzerindeki küçük ölçü farklılıkları, sorun olmaktan çıkar. Diyelim ki bir çarkın çevresi 60.1 santimetre, diğerininki ise 19.8 santimetre olsun. Burada iki çarkın birbirine oranı tam olarak 3:1 olmayacaktır. Ancak, çark üzerinde yer alacak diş sayısı ile çarkların birbirine orantısı kontrol edilip çarkların çevrelerindeki küçük farklılıklar, gözardı edilebilir.

Büyük dişli oranları yaratmak için, iki numaralı resimde görülen grup dişliler kullanılır.

Resimde sağ tarafta yer alan mor renkli grup dişli, aslında iki parçadan oluşur. Bir küçük ve bir büyük dişli, aynı eksende yer alacak şekilde, bir diğerinin üzerine yerleştirilmiştir. Mavi renkli dişlinin çevresi ile küçük olan mor renkli dişli çevresinin birbirlerine oranlarının 1:2 olduğunu varsayalım. Mavi dişli 1 tur döndüğünde, küçük olan mor dişli 2 tur dönecektir. Küçük olan mor dişli, alttaki büyük olan mor dişli ile birlikte hareket ettiğine göre (her iki mor dişliyi de aynı eksen üzerine sabitlemiştik) mavi dişli 1 tur dönerken büyük mor dişli 2 tur dönmüş olacak. Halbuki mavi ve büyük mor dişlinin çevreleri aynı! İşte grup dişlileri sihir gerçekleştirdi. Normalde mavi ve büyük mor dişliyi birbirlerine doğrudan temas ettirseydik, mavi bir tur atarken mor (büyük olan) da bir tur atacaktı. Büyük mor dişlinin üzerine bir adet küçük mor dişli takıp maviye temas ettirince alttaki büyük mor dişli, daha fazla tur attı.

Buna biraz daha karışık bir örnek verelim. Aslında o kadar karışık değil, sadece grup dişlilerin sayısını arttıracağız. Çünkü dişli kutularında, 3 numaralı resimde olduğu gibi, çoğunlukla birden çok grup dişlisi kullanılır.

3 numaralı resimdeki örnekte mor dişli, mavi dişlinin iki katı oranında tur atmaktadır. (Tekrar etmeye gerek var mı bilmiyorum ama yine de belirteyim: Mavi dişlinin çevresi, “küçük” mor dişlinin çevresinin 2 katıdır.) Aynı hesapla, yeşil dişli, mor dişlinin iki katı oranında tur atacaktır. Kırmızı dişli de yeşil dişlinin iki misli tur atmaktadır.

Şimdi örneğimizi değiştirelim ve 3 vitesli bir dişli kutusuna sahip olduğumuzu varsayalım. 4 numaralı resimde görülen dişli kutusundaki tüm dişli oranlarının 1’e 5 olduğunu kabul edelim. Bu durumda, dakikada 100 devir dönen bir motoru A dişlisine bağlarsak, B dişlisi, 1:5 oranı sebebiyle 500 kere dönecektir. C dişlisi de 2500 (5 x 500) tur atacaktır.

Pekiii, bu hesabı tersten yaparsak ne olur? Yani, dakikada 2.500 kere dönen bir motoru C dişlisine bağlarsak? A dişlisi100 kere döner dediğinizi duyar gibi oldum. (Dergi baskıdan çıktığından beri sürekli bir kulak çınlaması yaşıyorum doktor bey!)

çeşitlilik iyidir

Dişli çesiştleri bu kadarcık değil elbette ki. Hazır konuya girmişken fazla dağıtmadan bir iki değişik dişliden bahsedelim.

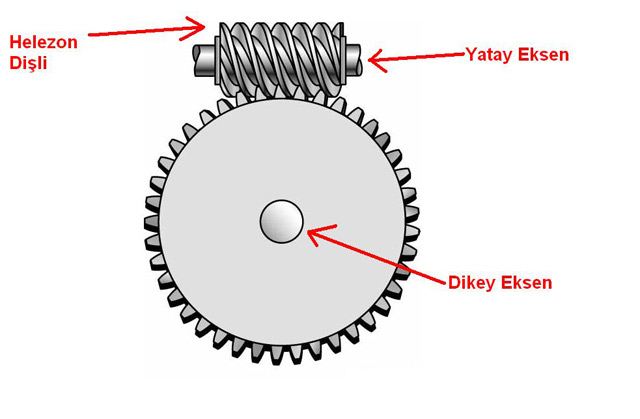
Eğer yüksek bir dişli oranı yaratmak istiyorsanız, helezon dişliler bu görevde çok başarılı olurlar. Helezon dişlilerin bir diğer özelliği, eksen açısını 90 derece (veya başka oranlarda) değiştirmenize imkan sağlamalarıdır. 5 numaralı resimde helezon dişli ve normal dişlinin nasıl hareket ettikleri ve bu iki dişlinin farklı açılardaki eksenlerini açıkça görebilirsiniz. Helezon dişlinin her 1 tur dönüşünde çark, 1 diş hareket edecektir. Çark üzerinde 40 adet diş olduğunu varsayarsak, çark dişlisinin helezon dişlisine oranı, 40’a 1 (40:1) olacaktır. Çok basit ve küçük bir düzenekle yüksek bir dişli oranı elde ettik. Kimi dişli kutularında, çark dişli grubu ve helezon dişliler birlikte kullanılırlar. 6 numaralı resim, buna güzel bir örnek. Resimdeki kutunun sağından çıkan eksende bir grup dişli birlikte kullanıldıktan sonra buradaki hareket, helezon dişli vasıtasıyla 90 derece açılı ikinci eksene yönlendirilmiş.

yön değişimi

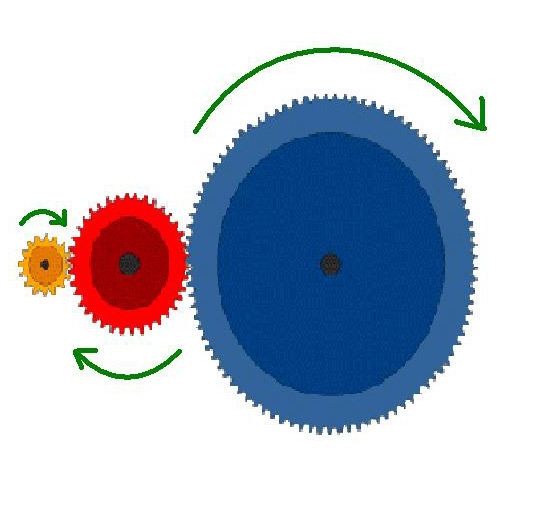
Pekiyi, bir başka soru: 6:1 dişli oranlı ama hareketin ilk çıktığı yön ile aynı yönde dönecek bir dişli kutusuna ihtiyacınız var. 7 numaralı resimde kullanılan yöntemle 3 adet dişli sayesinde bu isteğimizi gerçekleştirebiliriz. Mavi renkli dişli çapının (veya çevresinin) sarı renkli dişli çapından 6 kez büyük olması işimizi görecektir. Aradaki kırmızı renkli dişli çapının önemi yok; zira o dişli, sadece dönüş yönünü değiştirmek için kullanılıyor. Yani, mavi dişli saat yönünde dönerse, kırmızı dişli ters saat yönünde ve sarı dişli de tekrar saat yönünde dönecek, mavi ve sarı dişli aynı yönlerde dönmüş olacaklardır.

Kafanız yeterince karışmadıysa başka bir soruyla devam ediyorum: Birbirinden uzakta hareket eden iki adet dişliyi, aynı yönde ve eşgüdümlü (senkronize) çalıştırmak istersek düzeneğimiz nasıl olmalıdır? 8 numaralı resimde cevabı görebilirsiniz. İki adet kırmızı dişli, ortadaki mavi dişli sayesinde, birbirlerinden uzakta da olsalar eşgüdümlü ve aynı yönde dönebilmektedirler. Aynı kırmızı dişlileri farklı yönlere çevirmenin yöntemi ise 9 numaralı resimde yer almaktadır. Nasıl, basit değil mi?

ağırlık sorunsalı !!!

Ancak, her iki durumda da ilave dişli ve eksenler, gereksiz yere ağırlık yapacaklardır. İşte bu ağırlık sorununun çözümü, zincir veya dişli kayışlardır; hani motorumuzda yer alan zincir ve dişlileri hatırlarsınız ya! (Resim: 10)

Sonunda konuyu motorumuza bağlayabildiğimize göre kısa bir tarif yapalım: Şanzıman da denilen dişli kutusuna, motorun ürettiği hareket enerjisi, bir aks vasıtasıyla gelir. Bu aksın üzerinde bir dişli vardır ve bu dişli, bir ana grup dişliyi hareket ettirir. Ana grup dişli üzerindeki değişik çaptaki dişliler, başka eksenler üzerindeki değişik çaplı dişlilerle birleşerek değişik oranlarda hareket enerjisi üretirler. Ana grup ve yan grup dişlilerin hangilerinin birbiriyle birlikte çalışacaklarına, vites kolu sayesinde biz karar veririz. Vitesi yükselterek veya düşürerek değişik dişlilerin karşılıklı çalışmalarını sağlarız. Bu şekilde elde edilen hareket miktarı, son dişliye ulaşır. Son dişli, dişli kutusundan dışarı çıkan dişlidir ve zincir tahrikli motorlarda, zincirin önünde yer alan küçük dişlidir. Sonra bu küçük dişliyi, tekerleğin üzerindeki büyük dişliye zincirle bağlayıp, hareketi tekerleğe iletiriz.

soru neydi???

Şimdi gelelim sevgili okurumuzun sorusuna: vites oranları kısa, uzun ne demektir, bu kıyaslama neye göre yapılmaktadır diye sormuş kendisi. Her bir üretici, motosiklet motorunun en verimli ve etkili döndüğü hızı belirleyip motordan maksimum randımanı almak ister. Motorların beygirgücünü ve tork miktarını verdikleri belirli devir aralıkları vardır. Diyelim ki 5.000 devir bizim motorumuzun en randımanlı çalıştığı devir olsun. Bu devirdeki dönme hızını aynen tekerleğimize aktarırsak, tekerleğimizin 5.000 kere dönmesi gerekir ki bu da kara hız rekorunu motosikletle kırmaya eşdeğerdir. Halbuki motorumuzu bir anda değil yavaşça hızlandırır, hızımız arttıkça vites yükseltir ve hızlanmaya devam ederiz. Bu sebeple dişli kutusunu ve değişik oranlardaki dişlileri, vites kolu vasıtasıyla devreye sokarız.

Aynı motora iki ayrı vites kutusu taktığımızı varsayalım. Bunlardan bir tanesi birinci viteste 40:1, diğeri de 50:1 vites oranlarına sahip olsunlar. İlk motor 40 tur yaparken vites dişlisi 1 tur dönecek ve bu dönüş, son dişli ve zincir aracılığıyla tekerleğe iletilecektir. İkinci motorda ise 50 tur (daha yüksek devir) hareket ederken vites dişlisini 1 tur çevirecek ve yine buradaki hareket, tekerleğe iletilecektir. İlk motor galip gibi görünüyor değil mi? Pekiyi, ya motor freni yapmak istersek ne olacak? İlk motor, aynı devirde çalışırken motosikletimiz daha hızlı gideceği için ikinci motora göre dezavantajlı olacak. Ya yüklü bir motosikletle yokuş yukarı çıkıyorsak? Yine ikinci motor genellikle daha avantajlı olur çünkü yüksek devir ama az süratte daha yüksek tork elde edebiliriz. İkinci motor yine galip. Piste çıkıp yarışacaksak? Tabii ki ilk motor kazanır. Uzun lafın kısası, üreticiler, motorların hangi amaçla üretildiklerini ve hangi devirlerde en randımanlı çalıştıklarını hesaplayarak değişik vites kutuları hazırlıyorlar. Bir motorun 1. ve 2. viteslerinin diğer bir motora göre kısa olması, o motorun yüksek devirde daha az sürat yapması ama daha yüksek devir sayesinde daha çok yük taşıyabilmesi, bozuk yollarda yavaş ama devirli gitmeye imkan vermesi gibi değişik özellik ve avantajlar sağlayabilir. Kısa vites oranlı vites kutuları, ani hızlanmalarda faydalı olurken maksimum hızın düşük kalmasına yol açar. Uzun vites oranlarınız varsa, daha kısa vites oranlı motora göre ani hızalanamazsınız belki ama motorunuz devrini bulduğunda, yüksek süratlere erişirsiniz.

teknoloji nelere kadir?

Her şey fizik kuralları ve mühendislik hesaplarıyla ortaya çıkıyor. Fizik ve mühendislik, teknolojiyi de beraberinde taşıyor. Ancak teknoloji, doğru, verimli, çevreye ve çalışanlara zarar vermeden kullanıldığında faydalıdır. Charlie Chaplin’in ünlü sinema filmi Asri Zamanlar’ı seyrettiyseniz ne demek istediğimi daha iyi anlayacaksınız. Seyretmediyseniz bundan iyi bir fırsat olmaz; hemmen dergiyi okumayı tamamlayın ve filmi bulup seyredin. Unutmadan ekleyeyim: filmde bir sürü dişli ve çark var.